Sunday, April 30, 2006
Wednesday, April 26, 2006
2006 Bellevue BATH Competition.
Everyone in Washington should come to the first ever Bellevue BATH Competition! Details can be found here.
Monday, April 17, 2006
Sunday, April 16, 2006
Perimeter To Angle? Topic: Geometry/Trigonometry. Level: Olympiad.
Problem: (1986 China TST - #5) Given a square $ABCD$ whose side length is $1$, $P$ and $Q$ are points on the sides $AB$ and $AD$, respectively. If the perimeter of $APQ$ is $2$ find the angle $PCQ$.
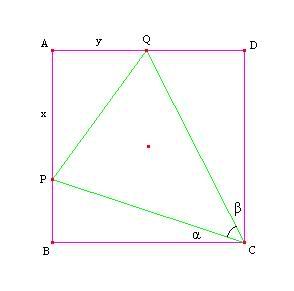
Solution: Let $ AP = x, AQ = y $ and $ \angle PCB = \alpha, \angle QCD = \beta $. By the given condition, we have $ AP+AQ+QP = x+y+\sqrt{x^2+y^2} = 2 $ (1). From this, we find
$ x+y = 2-\sqrt{x^2+y^2} $
$ (x+y)^2 = 4-4\sqrt{x^2+y^2}+(x^2+y^2) $
$ xy = 2-2\sqrt{x^2+y^2} $
Substituting $ \sqrt{x^2+y^2} = 2-x-y $ from (1), we have
$ xy = 2-2(2-x-y) \Rightarrow 2-x-y = x+y-xy \Rightarrow \frac{2-x-y}{x+y-xy} = 1 $ (2).
Note that $ \tan{\alpha} = \frac{PB}{BC} = 1-x $ and $ \tan{\beta} = \frac{QD}{DC} = 1-y $. Then
$ \tan{(\alpha+\beta)} = \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha} \cdot \tan{\beta}} = \frac{(1-x)+(1-y)}{1-(1-x)(1-y)} = \frac{2-x-y}{x+y-xy} $.
But by (2), we have $ \tan{(\alpha+\beta)} = \frac{2-x-y}{x+y-xy} = 1 \Rightarrow \alpha+\beta = 45^{\circ} $.
Hence $ \angle PCQ = 90^{\circ}-(\alpha+\beta) = 45^{\circ} $. QED.
--------------------
Comment: Trigonometry can come in handy quite often, especially when dealing with angles. Purely geometric solutions to this problem are a lot more complicated in my opinion; when in doubt, use algebra. The following identity comes in handy on quite a few problems.
--------------------
Practice Problem: Prove that in any triangle we have $ \tan{\frac{A}{2}} \cdot \tan{\frac{B}{2}} + \tan{\frac{B}{2}} \cdot \tan{\frac{C}{2}} + \tan{\frac{C}{2}} \cdot \tan{\frac{A}{2}} = 1 $.

Solution: Let $ AP = x, AQ = y $ and $ \angle PCB = \alpha, \angle QCD = \beta $. By the given condition, we have $ AP+AQ+QP = x+y+\sqrt{x^2+y^2} = 2 $ (1). From this, we find
$ x+y = 2-\sqrt{x^2+y^2} $
$ (x+y)^2 = 4-4\sqrt{x^2+y^2}+(x^2+y^2) $
$ xy = 2-2\sqrt{x^2+y^2} $
Substituting $ \sqrt{x^2+y^2} = 2-x-y $ from (1), we have
$ xy = 2-2(2-x-y) \Rightarrow 2-x-y = x+y-xy \Rightarrow \frac{2-x-y}{x+y-xy} = 1 $ (2).
Note that $ \tan{\alpha} = \frac{PB}{BC} = 1-x $ and $ \tan{\beta} = \frac{QD}{DC} = 1-y $. Then
$ \tan{(\alpha+\beta)} = \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha} \cdot \tan{\beta}} = \frac{(1-x)+(1-y)}{1-(1-x)(1-y)} = \frac{2-x-y}{x+y-xy} $.
But by (2), we have $ \tan{(\alpha+\beta)} = \frac{2-x-y}{x+y-xy} = 1 \Rightarrow \alpha+\beta = 45^{\circ} $.
Hence $ \angle PCQ = 90^{\circ}-(\alpha+\beta) = 45^{\circ} $. QED.
--------------------
Comment: Trigonometry can come in handy quite often, especially when dealing with angles. Purely geometric solutions to this problem are a lot more complicated in my opinion; when in doubt, use algebra. The following identity comes in handy on quite a few problems.
--------------------
Practice Problem: Prove that in any triangle we have $ \tan{\frac{A}{2}} \cdot \tan{\frac{B}{2}} + \tan{\frac{B}{2}} \cdot \tan{\frac{C}{2}} + \tan{\frac{C}{2}} \cdot \tan{\frac{A}{2}} = 1 $.
Saturday, April 15, 2006
That's A Lot Of Numbers. Topic: Logic/NT. Level: Olympiad.
Problem: (ACoPS 3.4.21) Initially, we are given the sequence $ 1,2, \ldots, 100 $. Every minute, we erase any two numbers $ u $ and $ v $ and replace them with the value $ uv+u+v $. Clearly, we will be left with just one number after $ 99 $ minutes. Does this number depend on the choices we made?
Solution: We claim that the number does not depend on the choices. Let $ a_1, a_2, \ldots, a_n $ be the numbers on the board after $ 100-n $ minutes. Define $ \displaystyle P_n = \prod_{i=1}^n (a_i+1) $. We claim that the sequence $ P_{100}, P_{99}, \ldots, P_1 $ is constant.
Noticing that $ (u+1)(v+1) = uv+u+v+1 $, we see that replacing $ u, v $ with $ uv+u+v+1 $ has no effect on the product $ P_n $. Indeed,
$ P_{k-1} = \frac{P_k(uv+u+v+1)}{(u+1)(v+1)} = P_k $
so we have $ P_{100} = P_{99} = \cdots = P_1 $ by induction. Since $ P_{100} $ is clearly constant, $ P_1 $ must be as well. Seeing that $ P_1 $ is equivalent to the remaining number, we conclude that it does not depend on the choices, as desired. QED.
--------------------
Comment: Problems with invariants require you to discover something (often a sum or product) that doesn't change with each step. The term $ uv+u+v $ should remind you of Simon's favorite factoring trick, leading to the invariant $ P_n $ as described above.
--------------------
Practice Problem: (ACoPS 3.4.23) Start with the set $ \{3,4,12\} $. You are then allowed to replace any two numbers $ a $ and $ b $ with the new pair $ 0.6a-0.8b $ and $ 0.8a+0.6b $. Can you transform the set into $ \{4,6,12\} $?
Solution: We claim that the number does not depend on the choices. Let $ a_1, a_2, \ldots, a_n $ be the numbers on the board after $ 100-n $ minutes. Define $ \displaystyle P_n = \prod_{i=1}^n (a_i+1) $. We claim that the sequence $ P_{100}, P_{99}, \ldots, P_1 $ is constant.
Noticing that $ (u+1)(v+1) = uv+u+v+1 $, we see that replacing $ u, v $ with $ uv+u+v+1 $ has no effect on the product $ P_n $. Indeed,
$ P_{k-1} = \frac{P_k(uv+u+v+1)}{(u+1)(v+1)} = P_k $
so we have $ P_{100} = P_{99} = \cdots = P_1 $ by induction. Since $ P_{100} $ is clearly constant, $ P_1 $ must be as well. Seeing that $ P_1 $ is equivalent to the remaining number, we conclude that it does not depend on the choices, as desired. QED.
--------------------
Comment: Problems with invariants require you to discover something (often a sum or product) that doesn't change with each step. The term $ uv+u+v $ should remind you of Simon's favorite factoring trick, leading to the invariant $ P_n $ as described above.
--------------------
Practice Problem: (ACoPS 3.4.23) Start with the set $ \{3,4,12\} $. You are then allowed to replace any two numbers $ a $ and $ b $ with the new pair $ 0.6a-0.8b $ and $ 0.8a+0.6b $. Can you transform the set into $ \{4,6,12\} $?
Friday, April 14, 2006
Move Those Stones. Topic: Logic. Level: AIME/Olympiad.
Problem: (TJ USAMO) Three piles of stones contain $100$, $2000$, and $2004$ stones respectively. If we are allowed to pick two of the piles and move one stone from each to the third pile, is it possible to eventually wind up with three piles of $1368$ stones?
Solution: Let $ a $ be the number of times the pile with $ 100 $ is the one that stones are added to. Similarly define $ b,c $ for the piles with $ 2000 $ and $ 2004 $, respectively. The number of stones in the piles are
$ 100+2a-(b+c) $, $ 2000+2b-(c+a) $, and $ 2004+2c-(a+b) $.
And these all have to equal $ 1368 $. So from the first two we have
$ 100+2a-(b+c) = 1368 \Rightarrow 2a-b-c = 1268 $ (1)
$ 2000+2b-(c+a) = 1368 \Rightarrow 2b-c-a = -632 $ (2).
Adding (1) and twice of (2), we have
$ (2a-b-c)+(4b-2c-2a) = 1268-1264 $
$ 3(b-c) = 4 $.
But this clearly is impossible, so the piles cannot end up with $ 1368 $ stones each. QED.
--------------------
Comment: This is basically an invariants problem, but working it out with a system of equations makes it even clearer that there is no solution. Most of the time, problems like this involve straightforward math but some tricky thinking.
Solution: Let $ a $ be the number of times the pile with $ 100 $ is the one that stones are added to. Similarly define $ b,c $ for the piles with $ 2000 $ and $ 2004 $, respectively. The number of stones in the piles are
$ 100+2a-(b+c) $, $ 2000+2b-(c+a) $, and $ 2004+2c-(a+b) $.
And these all have to equal $ 1368 $. So from the first two we have
$ 100+2a-(b+c) = 1368 \Rightarrow 2a-b-c = 1268 $ (1)
$ 2000+2b-(c+a) = 1368 \Rightarrow 2b-c-a = -632 $ (2).
Adding (1) and twice of (2), we have
$ (2a-b-c)+(4b-2c-2a) = 1268-1264 $
$ 3(b-c) = 4 $.
But this clearly is impossible, so the piles cannot end up with $ 1368 $ stones each. QED.
--------------------
Comment: This is basically an invariants problem, but working it out with a system of equations makes it even clearer that there is no solution. Most of the time, problems like this involve straightforward math but some tricky thinking.
Thursday, April 13, 2006
Cyclicity. Topic: Geometry. Level: Olympiad.
Problem: (1993 USAMO - #2) Let $ABCD$ be a convex quadrilateral such that diagonals $AC$ and $BD$ intersect at right angles, and let $E$ be their intersection. Prove that the reflections of $E$ across $AB, BC, CD, DA$ are concyclic.
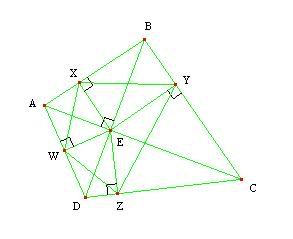
Solution: Let $ X,Y,Z,W $ be the feet of the perpendiculars from $ E $ to $ AB, BC, CD, DA $, respectively. Since the reflections of $ E $ across the sides are on lines $ EX, EY, EZ, EW $, just twice as far, we have $ XYZW $ similar to the quadrilateral formed by the reflections. Hence it is sufficient to show that $ XYZW $ is cyclic.
Consider quadrilaterals $ EWAX, EXBY, EYCZ, EZCW $. They are all cyclic because of the right angles formed at $ X,Y,Z,W $ (as shown in the diagram).
Thus we have $ \angle XWE = \angle XAE $, $ \angle ZWE = \angle ZDE $, $ \angle XYE = \angle XBE $, and $ \angle ZYE = \angle ZCE $.
Therefore, we have
$ \angle XWZ = \angle XWE + \angle ZWE = \angle XAE + \angle ZDE $
$ \angle XYZ = \angle XYE + \angle ZYE = \angle XBE + \angle ZCE $.
Also note that
$ \angle XAE + \angle XBE = 90^{\circ} $ and $ \angle ZDE + \angle ZCE = 90^{\circ} $ (1)
because the diagonals are perpendicular.
Finally,
$ \angle XWZ + \angle XYZ = (\angle XAE+\angle XBE)+(\angle ZDE+\angle ZCE) = 180^{\circ} $
by (1), which means $ XYZW $ is cyclic, as desired. QED.
--------------------
Comment: A decent amount of angle-chasing in this problem, but working it out wasn't bad. When you need to write all the steps in a proof, it can look a little messy and a little easy to get lost.
--------------------
Practice Problem: Given finitely many points in a plane, it is known that the area of the triangle formed by any three points of the set is less than $1$. Show that all points of the set lie inside or on boundary of a triangle with area less than $4$.

Solution: Let $ X,Y,Z,W $ be the feet of the perpendiculars from $ E $ to $ AB, BC, CD, DA $, respectively. Since the reflections of $ E $ across the sides are on lines $ EX, EY, EZ, EW $, just twice as far, we have $ XYZW $ similar to the quadrilateral formed by the reflections. Hence it is sufficient to show that $ XYZW $ is cyclic.
Consider quadrilaterals $ EWAX, EXBY, EYCZ, EZCW $. They are all cyclic because of the right angles formed at $ X,Y,Z,W $ (as shown in the diagram).
Thus we have $ \angle XWE = \angle XAE $, $ \angle ZWE = \angle ZDE $, $ \angle XYE = \angle XBE $, and $ \angle ZYE = \angle ZCE $.
Therefore, we have
$ \angle XWZ = \angle XWE + \angle ZWE = \angle XAE + \angle ZDE $
$ \angle XYZ = \angle XYE + \angle ZYE = \angle XBE + \angle ZCE $.
Also note that
$ \angle XAE + \angle XBE = 90^{\circ} $ and $ \angle ZDE + \angle ZCE = 90^{\circ} $ (1)
because the diagonals are perpendicular.
Finally,
$ \angle XWZ + \angle XYZ = (\angle XAE+\angle XBE)+(\angle ZDE+\angle ZCE) = 180^{\circ} $
by (1), which means $ XYZW $ is cyclic, as desired. QED.
--------------------
Comment: A decent amount of angle-chasing in this problem, but working it out wasn't bad. When you need to write all the steps in a proof, it can look a little messy and a little easy to get lost.
--------------------
Practice Problem: Given finitely many points in a plane, it is known that the area of the triangle formed by any three points of the set is less than $1$. Show that all points of the set lie inside or on boundary of a triangle with area less than $4$.
Wednesday, April 12, 2006
Hidden Triangle. Topic: Geometry/Inequalities. Level: Olympiad.
Problem: (TJ USAMO) Show that on any tetrahedron we can find a vertex $V$ such that the lengths of the $3$ edges with $V$ as an endpoint can be the sides of a triangle.
Solution: Call the tetrahedron $ ABCD $ and WLOG assume $ AB $ is the longest edge.
From triangle $ ABC $, we have $ BC+CA > AB $. From triangle $ ABD $, we have $ BD+DA > AB $. Summing the two inequalities together, we have
$ (BC+BD)+(CA+DA) > 2AB $.
It follows that one of $ BC+BD $ and $ CA+DA $ is greater than $ AB $. WLOG, assume $ CA+DA > AB $. But since $ AB $ is the longest edge and we have $ CA+DA > AB $, the edges $ AB $, $ AC $, and $ AD $ must form a triangle, as desired. QED.
-------------------
Comment: This problem was not too difficult; using the extremal principle to pick the longest side works well with triangles because as long as $ b+c > a $ when $ a $ is the largest of the three, $ a $, $ b $, and $ c $ can be the lengths of the sides of a triangle.
--------------------
Practice Problem: (TJ USAMO) Show that, for all positive reals $a$, $b$, and $c$ such that $a+b \ge c$; $b+c \ge a$; and $c+a \ge b$, we have
$2a^2(b + c) + 2b^2(c + a) + 2c^2(a + b) \ge a^3 + b^3 + c^3 + 9abc$.
When does equality hold?
Solution: Call the tetrahedron $ ABCD $ and WLOG assume $ AB $ is the longest edge.
From triangle $ ABC $, we have $ BC+CA > AB $. From triangle $ ABD $, we have $ BD+DA > AB $. Summing the two inequalities together, we have
$ (BC+BD)+(CA+DA) > 2AB $.
It follows that one of $ BC+BD $ and $ CA+DA $ is greater than $ AB $. WLOG, assume $ CA+DA > AB $. But since $ AB $ is the longest edge and we have $ CA+DA > AB $, the edges $ AB $, $ AC $, and $ AD $ must form a triangle, as desired. QED.
-------------------
Comment: This problem was not too difficult; using the extremal principle to pick the longest side works well with triangles because as long as $ b+c > a $ when $ a $ is the largest of the three, $ a $, $ b $, and $ c $ can be the lengths of the sides of a triangle.
--------------------
Practice Problem: (TJ USAMO) Show that, for all positive reals $a$, $b$, and $c$ such that $a+b \ge c$; $b+c \ge a$; and $c+a \ge b$, we have
$2a^2(b + c) + 2b^2(c + a) + 2c^2(a + b) \ge a^3 + b^3 + c^3 + 9abc$.
When does equality hold?
Tuesday, April 11, 2006
Every Difference Counts. Topic: Algebra/Sequences & Series/Sets. Level: Olympiad.
Problem: (TJ USAMO) Let $ x_1, x_2, x_3, \ldots $ be an infinite sequence of positive integers such that
$ x_1 = 1 $
$ x_i < x_{i+1} $ for all positive integers $ i $
$ x_{n+1} \le 2n $ for each $ n \ge 1 $.
Show that for any integer $ k $, there exist positive integers $ i $ and $ j $ such that $ k = x_i-x_j $.
Solution: If we show the result for positive $ k $, we can simply switch $ i $ and $ j $ to obtain the result for negative $ k $. The case $ k = 0 $ is simply any $ i = j $.
We claim that, for any positive integer $ k $, there exist positive integers $ i, j \le k+1 $ such that $ k = x_i-x_j $. Consider the set $ S_k = \{1,2,\ldots,2k\} $. The given conditions require that $ x_1, x_2, \ldots, x_{k+1} $ be distinct elements of $ S_k $.
We partition $ S_k $ into $ k $ different sets, as follows:
$ \{1,k+1\} $; $ \{2,k+2\} $; $\ldots$; $ \{k,2k\} $.
Since we have $ k+1 $ different elements and there are only $ k $ sets in the partition, by the Pigeonhole Principle two elements must be in the same set. Let $ x_i $ be the larger of the two and $ x_j $ be the smaller. Then we clearly have $ k = x_i-x_j $, as claimed.
$ k $ was arbitrarily chosen, so we know that it holds for all positive integers $ k $, completing the proof. QED.
--------------------
Comment: An interesting problem and good exercise in the Pigeonhole Principle. The application was subtle, yet upon seeing the solution very clear. Some hints may have been $ n+1 $ and $ 2n $ and the fact that we are looking for differences.
--------------------
Practice Problem: (TJ USAMO) $S$ is a set of eleven numbers are chosen from the set $ \{1, 2, . . ., 99, 100 \}$. Show that two disjoint, non-empty subsets of $S$ have the same sum.
$ x_1 = 1 $
$ x_i < x_{i+1} $ for all positive integers $ i $
$ x_{n+1} \le 2n $ for each $ n \ge 1 $.
Show that for any integer $ k $, there exist positive integers $ i $ and $ j $ such that $ k = x_i-x_j $.
Solution: If we show the result for positive $ k $, we can simply switch $ i $ and $ j $ to obtain the result for negative $ k $. The case $ k = 0 $ is simply any $ i = j $.
We claim that, for any positive integer $ k $, there exist positive integers $ i, j \le k+1 $ such that $ k = x_i-x_j $. Consider the set $ S_k = \{1,2,\ldots,2k\} $. The given conditions require that $ x_1, x_2, \ldots, x_{k+1} $ be distinct elements of $ S_k $.
We partition $ S_k $ into $ k $ different sets, as follows:
$ \{1,k+1\} $; $ \{2,k+2\} $; $\ldots$; $ \{k,2k\} $.
Since we have $ k+1 $ different elements and there are only $ k $ sets in the partition, by the Pigeonhole Principle two elements must be in the same set. Let $ x_i $ be the larger of the two and $ x_j $ be the smaller. Then we clearly have $ k = x_i-x_j $, as claimed.
$ k $ was arbitrarily chosen, so we know that it holds for all positive integers $ k $, completing the proof. QED.
--------------------
Comment: An interesting problem and good exercise in the Pigeonhole Principle. The application was subtle, yet upon seeing the solution very clear. Some hints may have been $ n+1 $ and $ 2n $ and the fact that we are looking for differences.
--------------------
Practice Problem: (TJ USAMO) $S$ is a set of eleven numbers are chosen from the set $ \{1, 2, . . ., 99, 100 \}$. Show that two disjoint, non-empty subsets of $S$ have the same sum.
Don't Be Such A Square. Topic: NT/Sequences & Series. Level: Olympiad.
Problem: (Math Olympiad Treasures - 3.4.6) The sequence $ (a_n)_{n \ge 0 } $ is defined by $ a_0 = a_1 = 1 $ and
$ a_{n+1} = 14a_n-a_{n-1} $
for all $ n \ge 1 $. Prove that the number $ 2a_n-1 $ is a square for all $ n \ge 0 $.
Solution: Define two new sequences $ (b_n)_{n \ge 0} $ by $ b_n = 2a_n-1 $ for $ n \ge 0 $ and $ (c_n)_{n \ge 0} $ by $ c_0 = -1, c_1 = 1 $ and $ c_{n+1} = 4c_n-c_{n-1} $ for $ n \ge 1 $. We claim that $ b_n = c_n^2 $ and since $ c_n $ is clearly a sequence of integers, this is the same as the desired result. Note that the recursion for $ b_n $ is $ b_{n+1} = 14b_n-b_{n+1}+12 $, which can be easily verified by substituting the $ b_n = 2a_n-1 $ back in.
First we will prove a lemma for the main proof. We claim that $ c_n^2+c_{n-1}^2 = 4c_nc_{n-1}+6 $ for all $ n \ge 1 $. We proceed by induction.
Base Case - $ c_1^2+c_0^2 = 4c_1c_0+6 \Leftrightarrow 1^2+(-1)^2 = 4(1)(-1)+6 \Leftrightarrow 2 = 2 $.
Induction Step - Suppose $ c_k^2+c_{k-1}^2 = 4c_kc_{k-1}+6 $. Then
$ c_{k+1}^2+c_k^2 = c_{k+1}^2+4c_kc_{k-1}-c_{k-1}^2+6 = c_{k+1}^2+c_{k-1}(4c_k-c_{k-1})+6 $.
Substituting $ c_{k+1} = 4c_k-c_{k-1} $ and $ c_{k-1} = 4c_k-c_{k+1} $, we have
$ c_{k+1}^2+c_k^2 = c_{k+1}^2+(4c_k-c_{k+1})c_{k+1}+6 $
$ c_{k+1}^2+c_k^2 = 4c_{k+1}c_k+6 $ (1),
completing the induction. Now we will use induction to prove that $ b_n = c_n^2 $ for $ n \ge 0 $.
Base Case - $ b_0 = c_0^2 \Leftrightarrow 1 = (-1)^2 \Leftrightarrow 1 = 1 $. $ b_1 = c_1^2 \Leftrightarrow 1 = 1^2 \Leftrightarrow 1 = 1 $.
Induction Step - Suppose $ b_k = c_k^2 $ and $ b_{k-1} = c_{k-1}^2 $. Then
$ b_{k+1} = 14b_k-b_{k-1}+12 = 14c_k^2-c_{k-1}^2+12 $.
Substituting $ c_{k-1} = 4c_k-c_{k+1} $ in, we have
$ b_{k+1} = 14c_k^2-(4c_k-c_{k+1})^2+12 $
$ b_{k+1} = 8c_{k+1}c_k-c_{k+1}^2-2c_k^2+12 $.
But from (1), we know $ c_{k+1}^2+c_k^2 = 4c_{k+1}c_k+6 \Rightarrow 8c_{k+1}c_k-c_{k+1}^2-2c_k^2+12 = c_{k+1}^2 $, so
$ b_{k+1} = c_{k+1}^2 $,
completing the induction. Hence we have shown that $ b_n = 2a_n-1 $ is always a square. QED.
--------------------
Comment: This proof required quite a few steps to finish, notably the two different induction steps necessary to prove the desired result. The motive for defining $ c_n $ was as usual looking at the first few terms, which happen to be $ -1, 1, 5, 19, 71 $. This pretty much gives it away and then all that's left is the proof.
--------------------
Practice Problem: (Math Olympiad Treasures - 3.4.5) Let $ x_1 = x_2 = 1, x_3 = 4 $ and
$ x_{n+3} = 2x_{n+2}+2x_{n+1}-x_n $
for all $ n \ge 1 $. Prove that $ x_n $ is a square for all $ n \ge 1 $.
$ a_{n+1} = 14a_n-a_{n-1} $
for all $ n \ge 1 $. Prove that the number $ 2a_n-1 $ is a square for all $ n \ge 0 $.
Solution: Define two new sequences $ (b_n)_{n \ge 0} $ by $ b_n = 2a_n-1 $ for $ n \ge 0 $ and $ (c_n)_{n \ge 0} $ by $ c_0 = -1, c_1 = 1 $ and $ c_{n+1} = 4c_n-c_{n-1} $ for $ n \ge 1 $. We claim that $ b_n = c_n^2 $ and since $ c_n $ is clearly a sequence of integers, this is the same as the desired result. Note that the recursion for $ b_n $ is $ b_{n+1} = 14b_n-b_{n+1}+12 $, which can be easily verified by substituting the $ b_n = 2a_n-1 $ back in.
First we will prove a lemma for the main proof. We claim that $ c_n^2+c_{n-1}^2 = 4c_nc_{n-1}+6 $ for all $ n \ge 1 $. We proceed by induction.
Base Case - $ c_1^2+c_0^2 = 4c_1c_0+6 \Leftrightarrow 1^2+(-1)^2 = 4(1)(-1)+6 \Leftrightarrow 2 = 2 $.
Induction Step - Suppose $ c_k^2+c_{k-1}^2 = 4c_kc_{k-1}+6 $. Then
$ c_{k+1}^2+c_k^2 = c_{k+1}^2+4c_kc_{k-1}-c_{k-1}^2+6 = c_{k+1}^2+c_{k-1}(4c_k-c_{k-1})+6 $.
Substituting $ c_{k+1} = 4c_k-c_{k-1} $ and $ c_{k-1} = 4c_k-c_{k+1} $, we have
$ c_{k+1}^2+c_k^2 = c_{k+1}^2+(4c_k-c_{k+1})c_{k+1}+6 $
$ c_{k+1}^2+c_k^2 = 4c_{k+1}c_k+6 $ (1),
completing the induction. Now we will use induction to prove that $ b_n = c_n^2 $ for $ n \ge 0 $.
Base Case - $ b_0 = c_0^2 \Leftrightarrow 1 = (-1)^2 \Leftrightarrow 1 = 1 $. $ b_1 = c_1^2 \Leftrightarrow 1 = 1^2 \Leftrightarrow 1 = 1 $.
Induction Step - Suppose $ b_k = c_k^2 $ and $ b_{k-1} = c_{k-1}^2 $. Then
$ b_{k+1} = 14b_k-b_{k-1}+12 = 14c_k^2-c_{k-1}^2+12 $.
Substituting $ c_{k-1} = 4c_k-c_{k+1} $ in, we have
$ b_{k+1} = 14c_k^2-(4c_k-c_{k+1})^2+12 $
$ b_{k+1} = 8c_{k+1}c_k-c_{k+1}^2-2c_k^2+12 $.
But from (1), we know $ c_{k+1}^2+c_k^2 = 4c_{k+1}c_k+6 \Rightarrow 8c_{k+1}c_k-c_{k+1}^2-2c_k^2+12 = c_{k+1}^2 $, so
$ b_{k+1} = c_{k+1}^2 $,
completing the induction. Hence we have shown that $ b_n = 2a_n-1 $ is always a square. QED.
--------------------
Comment: This proof required quite a few steps to finish, notably the two different induction steps necessary to prove the desired result. The motive for defining $ c_n $ was as usual looking at the first few terms, which happen to be $ -1, 1, 5, 19, 71 $. This pretty much gives it away and then all that's left is the proof.
--------------------
Practice Problem: (Math Olympiad Treasures - 3.4.5) Let $ x_1 = x_2 = 1, x_3 = 4 $ and
$ x_{n+3} = 2x_{n+2}+2x_{n+1}-x_n $
for all $ n \ge 1 $. Prove that $ x_n $ is a square for all $ n \ge 1 $.
Monday, April 10, 2006
Sum Square Function. Topic: Algebra/Sequences & Series. Level: Olympiad.
Problem: A function $f$ is defined for all positive integers and satisfies $f(1)=1996$, and $f(1)+f(2)+\cdots+f(n)=n^2f(n)$ for all $n>1$. Calculate the exact value of $f(1996)$.
Solution: Checking small values, we find $ f(2) = \frac{1996}{3} $, $ f(3) = \frac{1996}{6} $, and $ f(4) = \frac{1996}{10} $. The denominators look awfully like the triangular numbers, so we claim that
$ f(n) = \frac{2 \cdot 1996}{n(n+1)} $.
We will prove the result by strong induction.
Base Case - $ f(1) = 1996 $.
Induction Step - Assume that $ f(k) = \frac{2 \cdot 1996}{k(k+1)} $ for $ k = 1, \ldots, m $. We want to show that $ f(m+1) = \frac{2 \cdot 1996}{(m+1)(m+2)} $. From the given condition we have
$ f(1)+f(2)+\cdots+f(m)+f(m+1) = (m+1)^2f(m+1) $
$ \frac{2 \cdot 1996}{1 \cdot 2}+\frac{2 \cdot 1996}{2 \cdot 3}+\frac{2 \cdot 1996}{m(m+1)} = m(m+2)f(m+1) $.
Note that $ \frac{1}{k(k+1)} = \frac{1}{k}-\frac{1}{k+1} $, so the equation becomes
$ 2 \cdot 1996 \left( \frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{m}-\frac{1}{m+1} \right) = m(m+2)f(m+1) $
$ 2 \cdot 1996 \left(1-\frac{1}{m+1}\right) = m(m+2)f(m+1) $
$ 2 \cdot 1996 \left(\frac{m}{m+1}\right) = m(m+2)f(m+1) $,
which rearranges to
$ f(m+1) = \frac{2 \cdot 1996}{(m+1)(m+2)} $,
completing the induction. Hence $ f(1996) = \frac{2 \cdot 1996}{1996 \cdot 1997} = \frac{2}{1997} $. QED.
--------------------
Comment: Usually problems like these require you to play around with the problem for a while and once you think you see a pattern, conjecture it and hopefully prove it. Induction works well especially when they ask for a large value such as $ 1996 $.
--------------------
Practice Problem: If $ f(1) = k $, evaluate $ f(k) $ with the same condition in the above problem.
Solution: Checking small values, we find $ f(2) = \frac{1996}{3} $, $ f(3) = \frac{1996}{6} $, and $ f(4) = \frac{1996}{10} $. The denominators look awfully like the triangular numbers, so we claim that
$ f(n) = \frac{2 \cdot 1996}{n(n+1)} $.
We will prove the result by strong induction.
Base Case - $ f(1) = 1996 $.
Induction Step - Assume that $ f(k) = \frac{2 \cdot 1996}{k(k+1)} $ for $ k = 1, \ldots, m $. We want to show that $ f(m+1) = \frac{2 \cdot 1996}{(m+1)(m+2)} $. From the given condition we have
$ f(1)+f(2)+\cdots+f(m)+f(m+1) = (m+1)^2f(m+1) $
$ \frac{2 \cdot 1996}{1 \cdot 2}+\frac{2 \cdot 1996}{2 \cdot 3}+\frac{2 \cdot 1996}{m(m+1)} = m(m+2)f(m+1) $.
Note that $ \frac{1}{k(k+1)} = \frac{1}{k}-\frac{1}{k+1} $, so the equation becomes
$ 2 \cdot 1996 \left( \frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\cdots+\frac{1}{m}-\frac{1}{m+1} \right) = m(m+2)f(m+1) $
$ 2 \cdot 1996 \left(1-\frac{1}{m+1}\right) = m(m+2)f(m+1) $
$ 2 \cdot 1996 \left(\frac{m}{m+1}\right) = m(m+2)f(m+1) $,
which rearranges to
$ f(m+1) = \frac{2 \cdot 1996}{(m+1)(m+2)} $,
completing the induction. Hence $ f(1996) = \frac{2 \cdot 1996}{1996 \cdot 1997} = \frac{2}{1997} $. QED.
--------------------
Comment: Usually problems like these require you to play around with the problem for a while and once you think you see a pattern, conjecture it and hopefully prove it. Induction works well especially when they ask for a large value such as $ 1996 $.
--------------------
Practice Problem: If $ f(1) = k $, evaluate $ f(k) $ with the same condition in the above problem.
Sunday, April 9, 2006
Who's Game? Topic: Logic. Level: Olympiad.
Problem: (1999 USAMO - #5) The Y2K Game is played on a $1 \times 2000$ grid as follows. Two players in turn write either an S or an O in an empty square. The first player who produces three consecutive boxes that spell SOS wins. If all boxes are filled without producing SOS then the game is a draw. Prove that the second player has a winning strategy.
Strong: Let _ denote an open space.
We will show that the second player can always create an arrangement of squares such that the first player is forced to play a losing move. This arrangement is S _ _ S. If the first player plays an S, the second player can win with O. If the first player plays an O, the second player can win with S.
We claim that the second player can create the arrangement and not lose before the rest of the board is filled up, leaving on S _ _ S, which we established as a losing position for the first player. The second player may do this because there are en even number of total squares, so only the first player can face two empty squares.
Clearly if either player is faced with S O _, _ O S, or S _ S he wins; these are the winning positions. If the first player plays an O, the second player can play an O adjacent to it. This can never be a winning position for the first player because the winning positions require the O be have a _ and an S on both sides of it. If the first player plays an S, the second player may play an S adjacent to it unless it is one of the following arrangements:
S _ O _ or _ O _ S.
In either case, the second player simply plays an O between the existing S and O to leave no winning position.
The second player must make the first move far from the first player's first move, so as to leave open space to create the S _ _ S arrangement. Once that is done, assuming the first player does not give a winning position to the second player immediately, the first player will have two letters down, not enough to win. Hence the second player may play according to the above strategy until the only remaining spaces are the S _ _ S, which leaves the second player as the winner. QED.
--------------------
Comment: Game theory is a popular topic on the USAMO; mostly because it does not require in-depth techniques, but simply logic and proof-writing skills. It's also easy to overlook cases, so it weeds out the less rigorous competitors (which may be the case in my own proof...). We see that the 2000 is irrelevant here except that it is a large even number, important for the first move and the parity of turns.
--------------------
Practice Problem: (2004 USAMO - #4) Alice and Bob play a game on a 6 by 6 grid. On his or her turn, a player chooses a rational number not yet appearing in the grid and writes it in an empty square of the grid. Alice goes first and then the players alternate. When all squares have numbers written in them, in each row, the square with the greatest number in that row is colored black. Alice wins if she can then draw a line from the top of the grid to the bottom of the grid that stays in black squares, and Bob wins if she can't. (If two squares share a vertex, Alice can draw a line from one to the other that stays in those two squares.) Find, with proof, a winning strategy for one of the players.
Strong: Let _ denote an open space.
We will show that the second player can always create an arrangement of squares such that the first player is forced to play a losing move. This arrangement is S _ _ S. If the first player plays an S, the second player can win with O. If the first player plays an O, the second player can win with S.
We claim that the second player can create the arrangement and not lose before the rest of the board is filled up, leaving on S _ _ S, which we established as a losing position for the first player. The second player may do this because there are en even number of total squares, so only the first player can face two empty squares.
Clearly if either player is faced with S O _, _ O S, or S _ S he wins; these are the winning positions. If the first player plays an O, the second player can play an O adjacent to it. This can never be a winning position for the first player because the winning positions require the O be have a _ and an S on both sides of it. If the first player plays an S, the second player may play an S adjacent to it unless it is one of the following arrangements:
S _ O _ or _ O _ S.
In either case, the second player simply plays an O between the existing S and O to leave no winning position.
The second player must make the first move far from the first player's first move, so as to leave open space to create the S _ _ S arrangement. Once that is done, assuming the first player does not give a winning position to the second player immediately, the first player will have two letters down, not enough to win. Hence the second player may play according to the above strategy until the only remaining spaces are the S _ _ S, which leaves the second player as the winner. QED.
--------------------
Comment: Game theory is a popular topic on the USAMO; mostly because it does not require in-depth techniques, but simply logic and proof-writing skills. It's also easy to overlook cases, so it weeds out the less rigorous competitors (which may be the case in my own proof...). We see that the 2000 is irrelevant here except that it is a large even number, important for the first move and the parity of turns.
--------------------
Practice Problem: (2004 USAMO - #4) Alice and Bob play a game on a 6 by 6 grid. On his or her turn, a player chooses a rational number not yet appearing in the grid and writes it in an empty square of the grid. Alice goes first and then the players alternate. When all squares have numbers written in them, in each row, the square with the greatest number in that row is colored black. Alice wins if she can then draw a line from the top of the grid to the bottom of the grid that stays in black squares, and Bob wins if she can't. (If two squares share a vertex, Alice can draw a line from one to the other that stays in those two squares.) Find, with proof, a winning strategy for one of the players.
Saturday, April 8, 2006
Get Outta My Way! Topic: Algebra/Geometry/Sets. Level: AIME/Olympiad.
Problem: (Math Olympiad Treasures - 2.1.16) Seven reals numbers are given in the interval $ (1,13) $. Prove that at least three of them are the lengths of a triangle's sides.
Solution: Let $ x_1, x_2, \ldots, x_7 $ with $ x_1 \le x_2 \le \cdots \le x_7 $ be the reals. Suppose no three of them are the lengths of a triangle's sides. This means $ x_{i+2} \ge x_{i+1}+x_i $ for $ i = 1,2,\ldots,5 $.
We have $ x_2 \ge x_1 > 1 $. Then
$ x_3 \ge x_2+x_1 > 2 $.
Continuing this, we have
$ x_4 \ge x_3+x_2 > 3 $
$ x_5 \ge x_4+x_3 > 5 $
$ x_6 \ge x_5+x_4 > 8 $
$ x_7 \ge x_6+x_5 > 13 $,
a contradiction. Hence there must be three that are the length's of a triangle's sides. QED.
--------------------
Comment: From the proof we can easily see the generalization of $ n $ real numbers in the interval $ (1,F_n) $. This is a good example of a problem that doesn't really relate to geometry at all but the triangle condition is simply used as a way to restrict selection of the reals.
--------------------
Practice Problem: (Math Olympiad Treasures - 2.1.11) Consider $ n $ red and $ n $ blue points in the plane, no three of them being collinear. Prove that one can connect each red point to a blue point with a segment such that no two segments intersect.
Solution: Let $ x_1, x_2, \ldots, x_7 $ with $ x_1 \le x_2 \le \cdots \le x_7 $ be the reals. Suppose no three of them are the lengths of a triangle's sides. This means $ x_{i+2} \ge x_{i+1}+x_i $ for $ i = 1,2,\ldots,5 $.
We have $ x_2 \ge x_1 > 1 $. Then
$ x_3 \ge x_2+x_1 > 2 $.
Continuing this, we have
$ x_4 \ge x_3+x_2 > 3 $
$ x_5 \ge x_4+x_3 > 5 $
$ x_6 \ge x_5+x_4 > 8 $
$ x_7 \ge x_6+x_5 > 13 $,
a contradiction. Hence there must be three that are the length's of a triangle's sides. QED.
--------------------
Comment: From the proof we can easily see the generalization of $ n $ real numbers in the interval $ (1,F_n) $. This is a good example of a problem that doesn't really relate to geometry at all but the triangle condition is simply used as a way to restrict selection of the reals.
--------------------
Practice Problem: (Math Olympiad Treasures - 2.1.11) Consider $ n $ red and $ n $ blue points in the plane, no three of them being collinear. Prove that one can connect each red point to a blue point with a segment such that no two segments intersect.
Friday, April 7, 2006
Every Single One Of Them. Topic: Algebra/Sequences & Series. Level: Olympiad.
Problem: (Math Olympiad Treasures - 1.7.8) The sequence $ (x_n)_{n \ge 1} $ is defined by $ x_1 = 1 $, $ x_{2n} = 1+x_n $, and $ x_{2n+1} = \frac{1}{x_{2n}} $ for all $ n \ge 1 $. Prove that for any positive rational number $ r $ there exists a unique $ n $ such that $ r = x_n $.
Solution: Let $ r = \frac{p}{q} $. We will proceed by strong induction on $ q $. First note that $ x_{2n} > 1 $ and $ x_{2n+1} < 1 $ for $ n \ge 1 $.
Base Case: $ q = 1 $. Clearly all integers appear in the sequence uniquely because $ 1 $ does, so $ x_2 = 2, x_4 = 3, \ldots $ and their reciprocals can only appear as $ x_k $ when $ k $ is odd (by the comment above) so we will never have $ x_{2n+1} = \frac{1}{x_k} $ because $ k \neq 2n $.
Induction Step: So suppose $ r = \frac{p}{q} $. If $ p > q $, then repeatedly subtract $ q $ from $ p $ until $ p < q $. We can see that if $ \frac{p}{q} $ appears in the sequence we have $ \frac{p+kq}{q} $ in the sequence (from adding $ 1 $ repeatedly).
The only way that $ \frac{p}{q} $ can appear is if $ \frac{q}{p} $ appears. But since $ p < q $, our inductive hypothesis says that $ \frac{q}{p} $ is in the sequence already, so $ \frac{p}{q} $ must appear. And we know $ \frac{q}{p} $ only appears once (inductive hypothesis), so $ \frac{p}{q} $ can only appear once as well, completing the induction.
So we know that every positive rational number appears only once in the sequence, as desired. QED.
--------------------
Comment: This is a really cool sequence which generates the rational numbers and also provides a way of counting them. In actuality, a proof would need to be much more rigorous, but the details would be boring and not help in showing the insight required for this problem.
--------------------
Practice Problem: (Math Olympiad Treasures - 1.7.5) Let $ n $ be a positive integer. Prove that the number
$ 2^{2^n}-1 $
has at least $ n $ distinct prime divisors.
Solution: Let $ r = \frac{p}{q} $. We will proceed by strong induction on $ q $. First note that $ x_{2n} > 1 $ and $ x_{2n+1} < 1 $ for $ n \ge 1 $.
Base Case: $ q = 1 $. Clearly all integers appear in the sequence uniquely because $ 1 $ does, so $ x_2 = 2, x_4 = 3, \ldots $ and their reciprocals can only appear as $ x_k $ when $ k $ is odd (by the comment above) so we will never have $ x_{2n+1} = \frac{1}{x_k} $ because $ k \neq 2n $.
Induction Step: So suppose $ r = \frac{p}{q} $. If $ p > q $, then repeatedly subtract $ q $ from $ p $ until $ p < q $. We can see that if $ \frac{p}{q} $ appears in the sequence we have $ \frac{p+kq}{q} $ in the sequence (from adding $ 1 $ repeatedly).
The only way that $ \frac{p}{q} $ can appear is if $ \frac{q}{p} $ appears. But since $ p < q $, our inductive hypothesis says that $ \frac{q}{p} $ is in the sequence already, so $ \frac{p}{q} $ must appear. And we know $ \frac{q}{p} $ only appears once (inductive hypothesis), so $ \frac{p}{q} $ can only appear once as well, completing the induction.
So we know that every positive rational number appears only once in the sequence, as desired. QED.
--------------------
Comment: This is a really cool sequence which generates the rational numbers and also provides a way of counting them. In actuality, a proof would need to be much more rigorous, but the details would be boring and not help in showing the insight required for this problem.
--------------------
Practice Problem: (Math Olympiad Treasures - 1.7.5) Let $ n $ be a positive integer. Prove that the number
$ 2^{2^n}-1 $
has at least $ n $ distinct prime divisors.
Thursday, April 6, 2006
9th Degree? Topic: Algebra. Level: Olympiad.
Problem: (Math Olympiad Treasures - 1.4.8) Solve the equation
$ x+a^3 = \sqrt[3]{a-x} $,
where $ a $ is a real parameter.
Solution: We could cube and try to solve a cubic in $ x $ or a $ 9 $th degree polynomial in $ a $, but neither of those sound particularly easy or fun. Consider the function $ f(a) = x+a^3 $ in $ a $. We have $ f^{-1}(a) = \sqrt[3]{a-x} $.
Our given equation becomes $ f(a) = f^{-1}(a) \Rightarrow f(f(a)) = a $. We claim that $ f(a) = a $.
Suppose $ f(a) > a $. Since $ f $ is a strictly increasing function, we have $ f(f(a)) > f(a) > a $, contradiction. Similarly, if $ f(a) < a $ then $ f(f(a)) < f(a) < a $, another contradiction. Hence $ f(a) = a $, as claimed.
So it remains to solve $ x+a^3 = a $, which yields the only solution $ x = a-a^3 $. QED.
--------------------
Comment: This changing of variables required a little more ingenuity than the last one. Upon noticing that the two sides of the equation are in fact inverses of each other, proceeding from there is pretty simple. Discovering this fact is the key to solving the problem.
--------------------
Practice Problem: (Math Olympiad Treasures - 1.4.5) Let $ a \in \left(0,\frac{1}{4}\right) $. Solve the equation
$ \displaystyle x^2+2ax+\frac{1}{16} = -a+\sqrt{a^2+x-\frac{1}{16}} $.
$ x+a^3 = \sqrt[3]{a-x} $,
where $ a $ is a real parameter.
Solution: We could cube and try to solve a cubic in $ x $ or a $ 9 $th degree polynomial in $ a $, but neither of those sound particularly easy or fun. Consider the function $ f(a) = x+a^3 $ in $ a $. We have $ f^{-1}(a) = \sqrt[3]{a-x} $.
Our given equation becomes $ f(a) = f^{-1}(a) \Rightarrow f(f(a)) = a $. We claim that $ f(a) = a $.
Suppose $ f(a) > a $. Since $ f $ is a strictly increasing function, we have $ f(f(a)) > f(a) > a $, contradiction. Similarly, if $ f(a) < a $ then $ f(f(a)) < f(a) < a $, another contradiction. Hence $ f(a) = a $, as claimed.
So it remains to solve $ x+a^3 = a $, which yields the only solution $ x = a-a^3 $. QED.
--------------------
Comment: This changing of variables required a little more ingenuity than the last one. Upon noticing that the two sides of the equation are in fact inverses of each other, proceeding from there is pretty simple. Discovering this fact is the key to solving the problem.
--------------------
Practice Problem: (Math Olympiad Treasures - 1.4.5) Let $ a \in \left(0,\frac{1}{4}\right) $. Solve the equation
$ \displaystyle x^2+2ax+\frac{1}{16} = -a+\sqrt{a^2+x-\frac{1}{16}} $.
Wednesday, April 5, 2006
Partially Some! Topic: Algebra/Sequences & Series. Level: Olympiad.
Problem: Let $ a_1, a_2, \ldots, a_n $ be reals such that $ a_1+a_2+\cdots+a_n = 0 $. Show that there exists $ i \in \{1,2,\ldots,n\} $ such that $ a_i $, $ a_i+a_{i+1} $, $ \ldots $, $ a_i+a_{i+1}+\cdots+a_{i+n-1} $ are all nonnegative, where the indices are taken modulo $ n $.
Solution: Let $j$ be the value of $m$ for which the partial sum $a_1+a_2+\cdots+a_m$ is minimum ($m = 1,2,\ldots,n$). We claim that $i = j+1$ satisfies the property that $a_i$, $ a_i+a_{i+1} $, $\ldots$, $ a_i+a_{i+1}+\cdots+a_{i+n-1}$ are all nonnegative.
Suppose $a_i+a_{i+1}+\cdots+a_{i+k} < 0$. Then the partial sum
$a_1+a_2+\cdots+a_{i+k} < a_1+a_2+\cdots+a_{i-1} = a_1+a_2+\cdots+a_j$.
If $i+k > n$,
$ (a_1+a_2+\cdots+a_n)+a_{n+1}+a_{n+2}+\cdots+a_{i+k} = a_{n+1}+a_{n+2}+\cdots+a_{i+k} $.
Taking the indices modulo $ n $, we have
$ a_1+a_2+\cdots+a_{i+k-n} $,
which is also a partial sum. But we chose $j$ such that the partial sum was minimum, so we have a contradiction.
Hence none of the sums can be negative, as desired. QED.
--------------------
Comment: Playing around with numbers (and looking at graphs), it's not hard to conjecture the initial claim. Proving it rigorously came soon after by looking at partial sums.
--------------------
Practice Problem: For any finite set $A \subseteq \mathbb{R}$, define$ f(A) = \max(A) - \min(A) $. Take $S = \{1,2,\,\cdots,n\}$. Find $ \displaystyle \sum_{A \subseteq S} f(A)$.
Solution: Let $j$ be the value of $m$ for which the partial sum $a_1+a_2+\cdots+a_m$ is minimum ($m = 1,2,\ldots,n$). We claim that $i = j+1$ satisfies the property that $a_i$, $ a_i+a_{i+1} $, $\ldots$, $ a_i+a_{i+1}+\cdots+a_{i+n-1}$ are all nonnegative.
Suppose $a_i+a_{i+1}+\cdots+a_{i+k} < 0$. Then the partial sum
$a_1+a_2+\cdots+a_{i+k} < a_1+a_2+\cdots+a_{i-1} = a_1+a_2+\cdots+a_j$.
If $i+k > n$,
$ (a_1+a_2+\cdots+a_n)+a_{n+1}+a_{n+2}+\cdots+a_{i+k} = a_{n+1}+a_{n+2}+\cdots+a_{i+k} $.
Taking the indices modulo $ n $, we have
$ a_1+a_2+\cdots+a_{i+k-n} $,
which is also a partial sum. But we chose $j$ such that the partial sum was minimum, so we have a contradiction.
Hence none of the sums can be negative, as desired. QED.
--------------------
Comment: Playing around with numbers (and looking at graphs), it's not hard to conjecture the initial claim. Proving it rigorously came soon after by looking at partial sums.
--------------------
Practice Problem: For any finite set $A \subseteq \mathbb{R}$, define$ f(A) = \max(A) - \min(A) $. Take $S = \{1,2,\,\cdots,n\}$. Find $ \displaystyle \sum_{A \subseteq S} f(A)$.
Tuesday, April 4, 2006
Real Positive. Topic: Algebra/Inequalities/Sequences & Series. Level: Olympiad.
Problem: (Math Olympiad Treasures - 1.3.13) Suppose the sequence $ a_1, a_2, \ldots, a_n $ satisfies the following conditions:
$ a_1 = 0 $,$ |a_2| = |a_1+1| $, $ \ldots $, $ |a_n| = |a_{n-1}+1| $.
Prove that
$ \frac{a_1+a_2+\cdots+a_n}{n} \ge -\frac{1}{2} $.
Solution: Consider squaring the relations given in the sequence to obtain
$ a_2^2 = (a_1+1)^2 = a_1^2+2a_1+1 $
$ a_3^2 = (a_2+1)^2 = a_2^2+2a_2+1 $
$ \ldots $
$ a_{n+1}^2 = (a_n+1)^2 = a_n^2+2a_n+1 $.
Adding them up, we have
$ a_2^2+a_3^2+\cdots+a_{n+1}^2 = a_1^2+a_2^2+\cdots+a_n^2+2(a_1+a_2+\cdots+a_n)+n $, or
$ a_{n+1}^2 = 2(a_1+a_2+\cdots+a_n)+n \ge 0 $.
Then we have
$ \frac{a_1+a_2+\cdots+a_n}{n} \ge -\frac{1}{2} $,
as desired. QED.
--------------------
Comment: Absolute values are easy to get rid of by squaring things, usually giving us nice results. This method can be used in a variety of problems, but many times with sequences recursively defined we see it at its best. The following AIME problem can be solved this way.
--------------------
Practice Problem: (2006 AIME I - #15) Given that a sequence satisfies $x_0=0$ and $|x_k|=|x_{k-1}+3|$ for all integers $k\ge 1$, find the minimum possible value of $|x_1+x_2+\cdots+x_{2006}|$.
$ a_1 = 0 $,$ |a_2| = |a_1+1| $, $ \ldots $, $ |a_n| = |a_{n-1}+1| $.
Prove that
$ \frac{a_1+a_2+\cdots+a_n}{n} \ge -\frac{1}{2} $.
Solution: Consider squaring the relations given in the sequence to obtain
$ a_2^2 = (a_1+1)^2 = a_1^2+2a_1+1 $
$ a_3^2 = (a_2+1)^2 = a_2^2+2a_2+1 $
$ \ldots $
$ a_{n+1}^2 = (a_n+1)^2 = a_n^2+2a_n+1 $.
Adding them up, we have
$ a_2^2+a_3^2+\cdots+a_{n+1}^2 = a_1^2+a_2^2+\cdots+a_n^2+2(a_1+a_2+\cdots+a_n)+n $, or
$ a_{n+1}^2 = 2(a_1+a_2+\cdots+a_n)+n \ge 0 $.
Then we have
$ \frac{a_1+a_2+\cdots+a_n}{n} \ge -\frac{1}{2} $,
as desired. QED.
--------------------
Comment: Absolute values are easy to get rid of by squaring things, usually giving us nice results. This method can be used in a variety of problems, but many times with sequences recursively defined we see it at its best. The following AIME problem can be solved this way.
--------------------
Practice Problem: (2006 AIME I - #15) Given that a sequence satisfies $x_0=0$ and $|x_k|=|x_{k-1}+3|$ for all integers $k\ge 1$, find the minimum possible value of $|x_1+x_2+\cdots+x_{2006}|$.
Where Are They? Topic: Algebra. Level: Olympiad.
Problem: (Math Olympiad Treasures - 1.1.10) Find the locus of points $ (x,y) $ for which
$ x^3+y^3+3xy = 1 $.
Solution: Recall the useful factorization
$ a^3+b^3+c^3-3abc = \frac{1}{2}(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2] $.
Setting $ a = x $, $ b = y $, and $ c = -1 $, we obtain
$ x^3+y^3-1+3xy = \frac{1}{2}(x+y-1)[(x-y)^2+(y+1)^2+(-1-x)^2] $.
But from the given condition this expression is zero, so either
$ x+y-1 = 0 $,
which gives us the line $ x+y = 1 $ or
$ (x-y)^2+(y+1)^2+(-1-x)^2 = 0 $,
which gives us the point $ (-1,-1) $.
So the locus of points is the line $ x+y = 1 $ and $ (-1,-1) $. QED.
--------------------
Comment: The factorization basically finished the problem; it's nice to remember them because when they apply, they are extremely useful.
--------------------
Practice Problem: (Math Olympiad Treasures - 1.1.6) Let $ a,b,c $ be distinct real numbers. Prove that the following equality cannot hold:
$ \sqrt[3]{a-b}+\sqrt[3]{b-c}+\sqrt[3]{c-a} = 0 $.
$ x^3+y^3+3xy = 1 $.
Solution: Recall the useful factorization
$ a^3+b^3+c^3-3abc = \frac{1}{2}(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2] $.
Setting $ a = x $, $ b = y $, and $ c = -1 $, we obtain
$ x^3+y^3-1+3xy = \frac{1}{2}(x+y-1)[(x-y)^2+(y+1)^2+(-1-x)^2] $.
But from the given condition this expression is zero, so either
$ x+y-1 = 0 $,
which gives us the line $ x+y = 1 $ or
$ (x-y)^2+(y+1)^2+(-1-x)^2 = 0 $,
which gives us the point $ (-1,-1) $.
So the locus of points is the line $ x+y = 1 $ and $ (-1,-1) $. QED.
--------------------
Comment: The factorization basically finished the problem; it's nice to remember them because when they apply, they are extremely useful.
--------------------
Practice Problem: (Math Olympiad Treasures - 1.1.6) Let $ a,b,c $ be distinct real numbers. Prove that the following equality cannot hold:
$ \sqrt[3]{a-b}+\sqrt[3]{b-c}+\sqrt[3]{c-a} = 0 $.
Sunday, April 2, 2006
Absolutely! Topic: Algebra/Inequalities. Level: AIME/Olympiad.
Problem: Let $ a,b,c $ be reals such that $ |a| \ge |b+c| $, $ |b| \ge |c+a| $, and $ |c| \ge |a+b| $. Prove that $ a+b+c = 0 $.
Solution: WLOG, we may assume $ |a| \le |b| \le |c| $ because the problem is symmetric. Then $ |b+c| \le |a| \le |b| $ so $ b $ and $ c $ have opposite signs (either can be zero). Also $ |c+a| \le |b| \le |c| $ so $ a $ and $ c $ have opposite signs also (or zero). WLOG, assume $ a,b \le 0 $ and $ c \ge 0 $.
Now we proceed by contradiction. Suppose that $ a+b+c > 0 $ or $ a+b+c < 0 $.
CASE 1: $ a+b+c > 0 $
Then $ a+c > -b $ and both sides are positive so $ |a+c| > |b| $, contradiction.
CASE 2: $ a+b+c < 0 $
Then $ a+b < -c $ and both sides are negative so $ |a+b| > |c| $, contradiction.
Hence our assumption is false and we must have $ a+b+c = 0 $, as desired. QED.
--------------------
Comment: The idea was to exploit the symmetry of the problem effectively to bring about a contradiction. The algebra all works out nicely, too. For an alternative solution that preserves symmetry, try squaring the inequalities.
--------------------
Practice Problem: (1983 AIME - #2) Let $f(x)=|x-p|+|x-15|+|x-p-15|$, where $p \leq x \leq 15$. Determine the minimum value taken by $f(x)$ by $x$ in the interval $0 < p<15$.
Solution: WLOG, we may assume $ |a| \le |b| \le |c| $ because the problem is symmetric. Then $ |b+c| \le |a| \le |b| $ so $ b $ and $ c $ have opposite signs (either can be zero). Also $ |c+a| \le |b| \le |c| $ so $ a $ and $ c $ have opposite signs also (or zero). WLOG, assume $ a,b \le 0 $ and $ c \ge 0 $.
Now we proceed by contradiction. Suppose that $ a+b+c > 0 $ or $ a+b+c < 0 $.
CASE 1: $ a+b+c > 0 $
Then $ a+c > -b $ and both sides are positive so $ |a+c| > |b| $, contradiction.
CASE 2: $ a+b+c < 0 $
Then $ a+b < -c $ and both sides are negative so $ |a+b| > |c| $, contradiction.
Hence our assumption is false and we must have $ a+b+c = 0 $, as desired. QED.
--------------------
Comment: The idea was to exploit the symmetry of the problem effectively to bring about a contradiction. The algebra all works out nicely, too. For an alternative solution that preserves symmetry, try squaring the inequalities.
--------------------
Practice Problem: (1983 AIME - #2) Let $f(x)=|x-p|+|x-15|+|x-p-15|$, where $p \leq x \leq 15$. Determine the minimum value taken by $f(x)$ by $x$ in the interval $0 < p<15$.
Saturday, April 1, 2006
Crowded Interval. Topic: Inequalities/Sequences & Series. Level: Olympiad.
Problem: (2002 IMO Shortlist - A2) Let $a_1,a_2,\ldots$ be an infinite sequence of real numbers, for which there exists a real number $c$ with $0\le a_i\le c$ for all $i$, such that
$|a_i-a_j| \ge \frac{1}{i+j}$ for all $ i,j $ with $ i \neq j $.
Prove that $c \ge 1$.
Solution: Consider the finite subsequence $ a_1, a_2, \ldots, a_n $ for some positive integer $ n $. Let $ b_1, b_2, \ldots, b_n $ be a permutation of $ 1,2,\ldots,n $ such that $ a_{b_1} < a_{b_2} < \cdots < a_{b_n} $. This makes our consecutive differences all positive, so we don't need the absolute value signs anymore.
Consider the difference $ a_{b_n}-a_{b_1} $. We know that
$ a_{b_n}-a_{b_1} = \displaystyle \sum_{k=2}^n \left(a_{b_k}-a_{b_{k-1}}\right) $.
But from the given condition we have $ a_{b_k}-a_{b_{k-1}} \ge \frac{1}{b_k+b_{k-1}} $. So
$ a_{b_n}-a_{b_1} \ge \displaystyle \sum_{k=2}^n \frac{1}{b_k+b_{k-1}} $. (1)
By AM-HM or Cauchy, we have
$ \displaystyle \sum_{k=2}^n \frac{1}{b_k+b_{k-1}} \ge \frac{(n-1)^2}{b_1+2b_2+\cdots+2b_{n-1}+b_n} $. (2)
But because $ b_1+b_2+\cdots+b_n = \frac{n(n+1)}{2} $, we have
$ b_1+2b_2+\cdots+2b_{n-1}+b_n = n(n+1)-b_1-b_n < n^2+n-2 = (n+2)(n-1) $. (3)
Substituting (3) into (2) we have
$ \displaystyle \sum_{k=2}^n \frac{1}{b_k+b_{k-1}} > \frac{(n-1)^2}{(n+2)(n-1)} = \frac{n-1}{n+2} $. (4)
Substituting (4) into (1) we have
$ a_{b_n}-a_{b_1} > \frac{n-1}{n+2} $.
But taking $ n \rightarrow \infty $, the RHS can get arbitrarily close to $ 1 $, so
$ a_{b_n}-a_{b_1} \ge 1 $
$ a_{b_n} \ge 1+a_{b_1} $.
Finally, $ a_{b_1} \ge 0 $ so $ c \ge a_{b_n} \ge 1 $ as desired. QED.
--------------------
Comment: Taking a finite subsequence of an infinite sequence can be very helpful with inequalities, because it's easier to put some sort of bound on things. Arranging the terms in increasing order also allowed us to get rid of the absolute values.
--------------------
Practice Problem: (WOOT Test 8 - #6) Determine all positive real numbers $\alpha$ satisfying the following condition:
There exists a positive integer $n$ and a finite partition $A_1, A_2, . . ., A_n$ of the set of the positive integers such that each $A_i$ is infinite and such that if $x, y \in A_i$ with $ x \neq y $, then $ |x - y| \ge \alpha^i $.
$|a_i-a_j| \ge \frac{1}{i+j}$ for all $ i,j $ with $ i \neq j $.
Prove that $c \ge 1$.
Solution: Consider the finite subsequence $ a_1, a_2, \ldots, a_n $ for some positive integer $ n $. Let $ b_1, b_2, \ldots, b_n $ be a permutation of $ 1,2,\ldots,n $ such that $ a_{b_1} < a_{b_2} < \cdots < a_{b_n} $. This makes our consecutive differences all positive, so we don't need the absolute value signs anymore.
Consider the difference $ a_{b_n}-a_{b_1} $. We know that
$ a_{b_n}-a_{b_1} = \displaystyle \sum_{k=2}^n \left(a_{b_k}-a_{b_{k-1}}\right) $.
But from the given condition we have $ a_{b_k}-a_{b_{k-1}} \ge \frac{1}{b_k+b_{k-1}} $. So
$ a_{b_n}-a_{b_1} \ge \displaystyle \sum_{k=2}^n \frac{1}{b_k+b_{k-1}} $. (1)
By AM-HM or Cauchy, we have
$ \displaystyle \sum_{k=2}^n \frac{1}{b_k+b_{k-1}} \ge \frac{(n-1)^2}{b_1+2b_2+\cdots+2b_{n-1}+b_n} $. (2)
But because $ b_1+b_2+\cdots+b_n = \frac{n(n+1)}{2} $, we have
$ b_1+2b_2+\cdots+2b_{n-1}+b_n = n(n+1)-b_1-b_n < n^2+n-2 = (n+2)(n-1) $. (3)
Substituting (3) into (2) we have
$ \displaystyle \sum_{k=2}^n \frac{1}{b_k+b_{k-1}} > \frac{(n-1)^2}{(n+2)(n-1)} = \frac{n-1}{n+2} $. (4)
Substituting (4) into (1) we have
$ a_{b_n}-a_{b_1} > \frac{n-1}{n+2} $.
But taking $ n \rightarrow \infty $, the RHS can get arbitrarily close to $ 1 $, so
$ a_{b_n}-a_{b_1} \ge 1 $
$ a_{b_n} \ge 1+a_{b_1} $.
Finally, $ a_{b_1} \ge 0 $ so $ c \ge a_{b_n} \ge 1 $ as desired. QED.
--------------------
Comment: Taking a finite subsequence of an infinite sequence can be very helpful with inequalities, because it's easier to put some sort of bound on things. Arranging the terms in increasing order also allowed us to get rid of the absolute values.
--------------------
Practice Problem: (WOOT Test 8 - #6) Determine all positive real numbers $\alpha$ satisfying the following condition:
There exists a positive integer $n$ and a finite partition $A_1, A_2, . . ., A_n$ of the set of the positive integers such that each $A_i$ is infinite and such that if $x, y \in A_i$ with $ x \neq y $, then $ |x - y| \ge \alpha^i $.
Subscribe to:
Posts (Atom)