Cyclicity. Topic: Geometry. Level: Olympiad.

Problem: (1993 USAMO - #2) Let $ABCD$ be a convex quadrilateral such that diagonals $AC$ and $BD$ intersect at right angles, and let $E$ be their intersection. Prove that the reflections of $E$ across $AB, BC, CD, DA$ are concyclic.



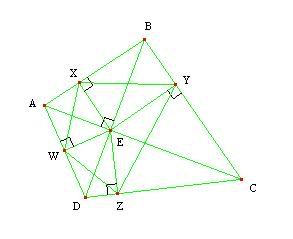
Solution: Let $ X,Y,Z,W $ be the feet of the perpendiculars from $ E $ to $ AB, BC, CD, DA $, respectively. Since the reflections of $ E $ across the sides are on lines $ EX, EY, EZ, EW $, just twice as far, we have $ XYZW $ similar to the quadrilateral formed by the reflections. Hence it is sufficient to show that $ XYZW $ is cyclic.

Consider quadrilaterals $ EWAX, EXBY, EYCZ, EZCW $. They are all cyclic because of the right angles formed at $ X,Y,Z,W $ (as shown in the diagram).

Thus we have $ \angle XWE = \angle XAE $, $ \angle ZWE = \angle ZDE $, $ \angle XYE = \angle XBE $, and $ \angle ZYE = \angle ZCE $.

Therefore, we have

$ \angle XWZ = \angle XWE + \angle ZWE = \angle XAE + \angle ZDE $

$ \angle XYZ = \angle XYE + \angle ZYE = \angle XBE + \angle ZCE $.

Also note that

$ \angle XAE + \angle XBE = 90^{\circ} $ and $ \angle ZDE + \angle ZCE = 90^{\circ} $ (1)

because the diagonals are perpendicular.

Finally,

$ \angle XWZ + \angle XYZ = (\angle XAE+\angle XBE)+(\angle ZDE+\angle ZCE) = 180^{\circ} $

by (1), which means $ XYZW $ is cyclic, as desired. QED.

--------------------

Comment: A decent amount of angle-chasing in this problem, but working it out wasn't bad. When you need to write all the steps in a proof, it can look a little messy and a little easy to get lost.

--------------------

Practice Problem: Given finitely many points in a plane, it is known that the area of the triangle formed by any three points of the set is less than $1$. Show that all points of the set lie inside or on boundary of a triangle with area less than $4$.