Perimeter To Angle? Topic: Geometry/Trigonometry. Level: Olympiad.

Problem: (1986 China TST - #5) Given a square $ABCD$ whose side length is $1$, $P$ and $Q$ are points on the sides $AB$ and $AD$, respectively. If the perimeter of $APQ$ is $2$ find the angle $PCQ$.



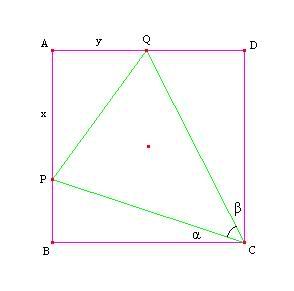
Solution: Let $ AP = x, AQ = y $ and $ \angle PCB = \alpha, \angle QCD = \beta $. By the given condition, we have $ AP+AQ+QP = x+y+\sqrt{x^2+y^2} = 2 $ (1). From this, we find

$ x+y = 2-\sqrt{x^2+y^2} $

$ (x+y)^2 = 4-4\sqrt{x^2+y^2}+(x^2+y^2) $

$ xy = 2-2\sqrt{x^2+y^2} $

Substituting $ \sqrt{x^2+y^2} = 2-x-y $ from (1), we have

$ xy = 2-2(2-x-y) \Rightarrow 2-x-y = x+y-xy \Rightarrow \frac{2-x-y}{x+y-xy} = 1 $ (2).

Note that $ \tan{\alpha} = \frac{PB}{BC} = 1-x $ and $ \tan{\beta} = \frac{QD}{DC} = 1-y $. Then

$ \tan{(\alpha+\beta)} = \frac{\tan{\alpha}+\tan{\beta}}{1-\tan{\alpha} \cdot \tan{\beta}} = \frac{(1-x)+(1-y)}{1-(1-x)(1-y)} = \frac{2-x-y}{x+y-xy} $.

But by (2), we have $ \tan{(\alpha+\beta)} = \frac{2-x-y}{x+y-xy} = 1 \Rightarrow \alpha+\beta = 45^{\circ} $.

Hence $ \angle PCQ = 90^{\circ}-(\alpha+\beta) = 45^{\circ} $. QED.

--------------------

Comment: Trigonometry can come in handy quite often, especially when dealing with angles. Purely geometric solutions to this problem are a lot more complicated in my opinion; when in doubt, use algebra. The following identity comes in handy on quite a few problems.

--------------------

Practice Problem: Prove that in any triangle we have $ \tan{\frac{A}{2}} \cdot \tan{\frac{B}{2}} + \tan{\frac{B}{2}} \cdot \tan{\frac{C}{2}} + \tan{\frac{C}{2}} \cdot \tan{\frac{A}{2}} = 1 $.