$ A_1B_1 \cdot B_1C_1 \cdot C_1A_1 \ge A_1B \cdot B_1C \cdot C_1A $.
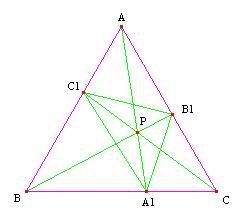
Solution: First thing to take into account is the fact that the triangle is equilateral. There is probably a good reason for this, so let's try and find it. Applying the Law of Cosines on triangle $ A_1B_1C $, we find
$ (A_1B_1)^2 = (A_1C)^2+(B_1C)^2-A_1C \cdot B_1C $.
But since $ (A_1C-B_1C)^2 \ge 0 \Rightarrow (A_1C)^2+(B_1C)^2-A_1C \cdot B_1C \ge A_1C \cdot B_1C $, we have
$ (A_1B_1)^2 \ge A_1C \cdot B_1C $.
Similarly, $ (B_1C_1)^2 \ge B_1A \cdot C_1A $ and $ (C_1A_1)^2 \ge C_1B \cdot A_1B $. Multiplying these three inequalities together, we obtain
$ (A_1B_1 \cdot B_1C_1 \cdot C_1A_1)^2 \ge (A_1B \cdot B_1C \cdot C_1A)(A_1C \cdot B_1A \cdot C_1B) $.
But by Ceva's, we know $ A_1B \cdot B_1C \cdot C_1A = A_1C \cdot B_1A \cdot C_1B $, so
$ (A_1B_1 \cdot B_1C_1 \cdot C_1A_1)^2 \ge (A_1B \cdot B_1C \cdot C_1A)^2 $
and
$ A_1B_1 \cdot B_1C_1 \cdot C_1A_1 \ge A_1B \cdot B_1C \cdot C_1A $
as desired. QED.
--------------------
Comment: After we were able to figure out an effective way to use the equilateral condition, it wasn't hard to see the inequality there. Then the problem just asks for Ceva, which fits in nicely at the end.
--------------------
Practice Problem: (1996 USAMO - #5) Let $ABC$ be a triangle, and $M$ an interior point such that $\angle MAB=10^\circ$, $\angle MBA=20^\circ$, $\angle MAC=40^\circ$, and $\angle MCA=30^\circ$. Prove that the triangle is isosceles.
No comments:
Post a Comment