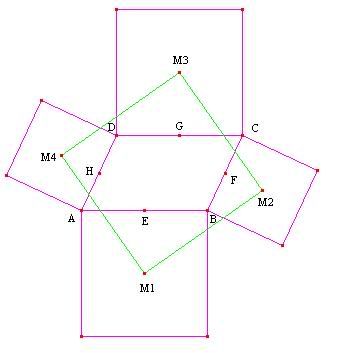
Solution: We will show a solution using complex numbers. In general, the lower case of a letter that represents a point is the complex number it corresponds to. Assume WLOG that $ A $ is at the origin, or $ a = 0 $. Then $ b $ and $ d $ are arbitrary complex numbers. Since it is a parallelogram $ c = b+d $.
$ E,F,G,H $ are the midpoints of $ AB, BC, CD, DA $, respectively, so
$ e = \frac{b}{2} $, $ f = b+\frac{d}{2} $, $ g = d+\frac{b}{2} $, and $ h = \frac{d}{2} $.
$ M_1 $ is equivalent to $ A $ rotated $ \frac{\pi}{2} $ clockwise around $ E $. In complex numbers this translates to
$ m_1 = e+(a-e)i = \frac{b}{2}-\frac{b}{2}i $.
Similarly,
$ m_2 = f+(b-f)i = \left(b+\frac{d}{2}\right)-\frac{d}{2}i $
$ m_3 = g+(c-g)i = \left(d+\frac{b}{2}\right)+\frac{b}{2}i $
$ m_4 = h+(d-h)i = \frac{d}{2}+\frac{d}{2}i $.
We want to show that these form a square, so if we rotate $ M_1 $ clockwise $ \frac{\pi}{2} $ around $ M_4 $ we should end up with $ M_3 $, and similarly for the other sets of three vertices.
Verifying that
$ m_4+(m_1-m_4)i = m_3 $
$ m_1+(m_2-m_1)i = m_4 $
$ m_2+(m_3-m_2)i = m_1 $
$ m_3+(m_4-m_3)i = m_2 $,
we know that $ M_1M_2M_3M_4 $ is indeed a square. QED.
--------------------
Comment: Complex numbers are often useful when a problem involves showing something is a square or an equilateral triangle because those rotations in the complex plane come out nicely. Sometimes the calculations can be tedious, but if geometry isn't your strong point, complex numbers is an effective way of reducing a geometry problem to an algebra one.
--------------------
Problem: (Problem-Solving Through Problems) Let $ z_1, z_2, z_3 $ be complex numbers. Show that $ z_1, z_2, z_3 $ form an equilateral triangle if and only if
$ z_1^2+z_2^2+z_3^2 = z_1z_2+z_2z_3+z_3z_1 $.
No comments:
Post a Comment