That's The Orthocenter! Topic: Geometry/Inequalities. Level: Olympiad.

Problem: (360 Problems For Mathematical Contests - 3.1.7) Let $ a,b,c $ and $ S $ be the side lengths and the area of triangle $ ABC $. Prove that if $ P $ is a point interior to triangle $ ABC $ such that

$ a \cdot PA+b \cdot PB+c \cdot PC = 4S $

then $ P $ is the orthocenter of the triangle.



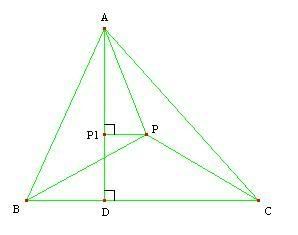
Solution: Let $ D, E, F $ be the feet of the altitudes from $ A, B, C $ respectively. Denote $ P_1, P_2, P_3 $ the projections of $ P $ onto $ AD, BE, CF $, respectively. $ D $ and $ P_1 $ are shown in the picture above.

We know $ S = [PBC]+[PCA]+[PAB] $. And since the altitudes of these three smaller triangles from $ P $ are equal in length to $ P_1D = AD-AP_1 $, $P_2E = BE-BP_2 $, $ P_3F = CF-CP_3 $, respectively, we have

$ [PBC] = \frac{1}{2}a(AD-AP_1) $

$ [PCA] = \frac{1}{2}b(BE-BP_2) $

$ [PAB] = \frac{1}{2}c(CF-CP_2) $.

So $ S = \frac{1}{2}(a \cdot AD+ b \cdot BE+ c \cdot CF) - \frac{1}{2}(a \cdot AP_1 + b \cdot BP_2 + c \cdot CP_3) $, which rearranges to

$ a \cdot AP_1+ b \cdot BP_2 + c\cdot CP_3 = a \cdot AD+ b \cdot BE+ c \cdot CF - 2S $. (1)

But since $ \frac{1}{2} a \cdot AD = \frac{1}{2} b \cdot BE = \frac{1}{2} c \cdot CF = S $, we have

$ a \cdot AD + b \cdot BE + c \cdot CF = 6S $. (2)

Substituting (2) into (1), we obtain

$ a \cdot AP_1+ b \cdot BP_2 + c\cdot CP_3 = 6S-2S = 4S $.

However, we have $ AP \ge AP_1 $, $ BP \ge BP_2 $, and $ CP \ge CP_3 $ (since they are projections) so

$ a \cdot AP + b \cdot BP + c \cdot CP \ge a \cdot AP_1+ b \cdot BP_2 + c\cdot CP_3 = 4S $.

But since the given condition implies equality, we know that $ AP = AP_1 $, $ BP = BP_2 $, and $ CP = CP_3 $, or that $ P $ lies on all three altitudes it was projected on and hence is the orthocenter. QED.

--------------------

Comment: Many times geometric conditions often arise from inequalities that have a specific equality case. In this problem, we wanted to show something was the orthocenter so we related the given lengths to the altitudes, which worked.

--------------------

Practice Problem: (360 Problems For Mathematical Contests - 3.1.14) Let $ I $ be the incenter of an acute triangle $ ABC $. Prove that

$ AI \cdot BC + BI \cdot CA + CI \cdot AB = 4S_{ABC} $

if and only if triangle $ ABC $ is equilateral.